Massively Parallel Solvers
Designed to take full advantage of today's most powerful petascale supercomputers
Iterative
Parallel sparse linear solver
The ESPRESO framework contains several highly scalable solvers based on the methods of domain decomposition which allows the computational capacity of the state-of-the-art supercomputers to be fully utilized and thus solve problems with billions of unknowns.
CPU version
for Massively Parallel systems
GPU version
Nvidia GPU accelerated version for systems with hybrid architectures
Automatic tuning
solver setting by evolutionary and swarm optimisation algorithms
Strong scalability - elasticity problem
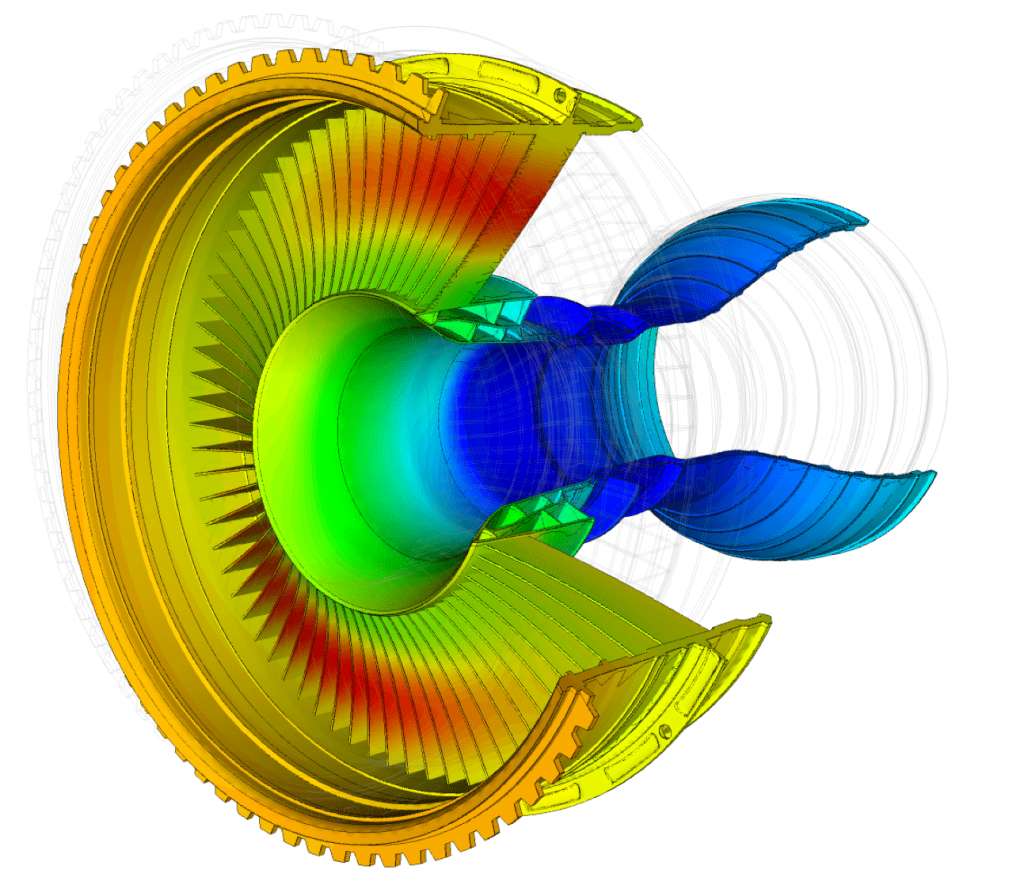
300 Million unknowns Jet Engine case
Successfully Tested on large Peta-scale machines
Largest problem solved by ESPRESO in 160 seconds
The ESPRESO solver is an in-house developed highly efficient parallel solver that contains several FETI based algorithms including the Hybrid Total FETI method suitable for parallel machines with tens or hundreds of thousands of cores. The solver is based on a highly efficient communication layer on top of MPI. It is not just an MPI code but, as many modern parallel applications, it uses the hybrid parallelization. The three levels of parallelization are message passing, threading using OpenMP, and vectorization using Intel MKL and OpenMP.
Hybrid solver strong scalability
Heat transfer
20 billion unknowns
Elasticity
11 bilion unknowns
We also offer our massively parallel solver as a third party library. To interface ESPRESO with the third party software, a general API has been implemented. The API has been successfully used to connect ESPRESO with the Elmer. Even though ESPRESO is C++ library, the API uses plain C only. Hence, it is easy to use it with various other languages such as Fortran.
Quadratic programming
Scalable nonlinear solvers
For nonlinear problems with equality and inequality conditions, we implement an in-house solver based on quadratic programming problems. This solver in combination with domain decomposition techniques gives users the possibility to solve contact problems in parallel with almost linear complexity
semi-monotonic augmented Lagrangian method with separable convex constraints and general equality constraints
modified proportioning with reduced gradient projection
In-house constrained QP algorithm
We combine an augmented Lagrangian based solver with active set reflecting restarted preconditioned conjugate gradients in the inner loop, and FETI based domain decomposition techniques. Consequently we are able to solve especially large contact problems efficiently on HPC infrastructures.

Available third party solvers
For highly heterogenous systems, algebraic multigrid or direct solvers can be used for solving defined problems.